meta data for this page
정규분포 (Normal Distribution)
정의
기원
정규분포는 드무아브르가 1733년 쓴 글에서 특정 이항분포의 n이 클 때 그 분포의 근사치를 계산하는 것과 관련하여 처음 소개되었고 이 글은 그의 저서 《우연의 교의》 2판(1738년)에 다시 실렸다. 라플라스는 그의 저서 《확률론의 해석이론》(1812년)에서 이 결과를 확장하였고 이는 오늘날 드무아브르-라플라스의 정리로 알려져있다.
라플라스는 실험 오차를 분석하면서 정규분포를 사용했다. 1805년에는 르장드르가 매우 중요한 방법인 최소 제곱법을 도입했다. 가우스는 이 방법을 1794년부터 사용해왔다고 주장했는데 1809년에는 실험 오차가 정규분포를 따른다는 가정하에 최소 제곱법을 이론적으로 엄밀히 정당화했다.
이 분포가 최초의 발견자 이름을 따지 않고 가우스 분포로 불리는 것은 과학적 발견은 그 최초 발견자의 이름을 따지 않는다는 스티글러의 명명법칙의 한 예이다.
표기
확률변수 $X$가 평균 $\mu$, 분산 $\sigma^{2}$을 갖는 정규분포라 한다면 아래와 같이 표기 한다.
- $$ X \sim N(\mu , \sigma^{2})$$
- $$ \mu \in ( \ - \infty \ , \ \infty \ ) $$
- $$ \sigma^{2} \in ( \ 0 \ , \ \infty \ ) $$
받침
$$ x \in ( \ - \infty \ , \ \infty \ ) $$
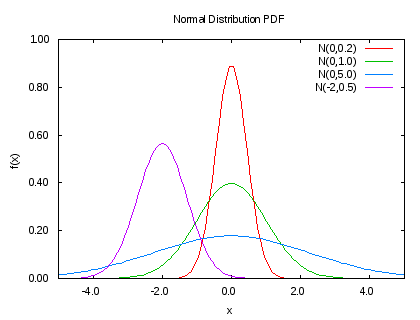
확률밀도함수
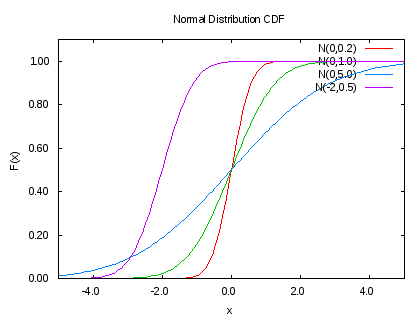
누적분포함수
$$ F(x) = \frac{1}{2} \left[ 1 + \mathrm{erf} \left( \frac{x - \mu}{\sigma \sqrt{2}} \right) \right] $$
- 단, $\mathrm{erf}(x)$ 는 오차함수
기대값
$$E(X)=\mu$$
중앙값
$$ Mdn = \mu $$
최빈값
$$ Mo = \mu $$
분산
$$Var(X)=\sigma^{2}$$
왜도
$$ \gamma_{1} = 0 $$
첨도
$$ \gamma_{2} = 0 $$
특성함수
$$ \phi \ (t) = \exp \left( \mu \ i \ t - \frac{\sigma^{2} t^{2}}{2} \right) $$
적률생성함수
$$ M(t) = \exp \left( \mu \ t + \frac{\sigma^{2} t^{2}}{2} \right) $$
$$ M'(t) = (\mu + \sigma^{2} t) \cdot \exp \left[ \mu t + \sigma^{2} t^{2} / 2 \right] $$
$$ M''(t) = \left[ \sigma^{2} + (\mu + \sigma^{2} t)^{2} \right] \cdot \exp \left[ \mu t + \sigma^{2} t^{2} / 2 \right] $$
원적률
$$ \mu'_{0} = 1 $$
$$ \mu'_{1} = \mu $$
$$ \mu'_{2} = \mu^{2} + \sigam^{2} $$
$$ \mu'_{3} = \mu^{3} + 3 \mu \sigma^{2} $$
$$ \mu'_{4} = \mu^{4} + 6 \mu^{2} \sigma^{2} + 3 \sigma^{4} $$
중심적률
$$ \mu_{1} = 0 $$
$$ \mu_{2} = \sigma^{2} $$
$$ \mu_{3} = 0 $$
$$ \mu_{4} = 3 \sigma^{4} $$
특징
- 재생성을 가진다.
- $X_{i} \sim N(\mu_{i},\sigma_{i}^{2})$이면 $\sum X_{i} \sim N(\sum \mu_{i},\sum \sigma_{i}^{2})$이 성립한다.