meta data for this page
표준정규분포 (Standard Normal Distribution)
정의
표기
받침
$$ x \in ( \ - \infty \ , \ \infty \ ) $$
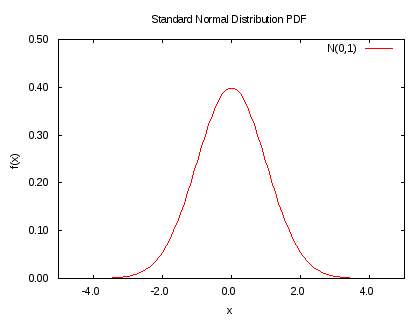
확률밀도함수
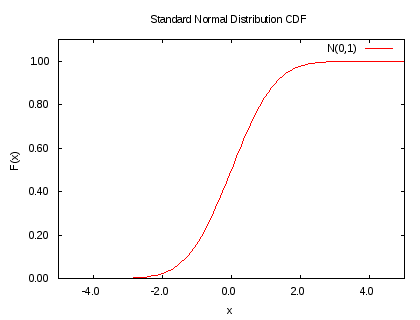
누적분포함수
$$ F(x) = \frac{1}{2} \left[ 1 + \mathrm{erf} \left( \frac{x}{\sqrt{2}} \right) \right] $$
단, $\mathrm{erf}(x)$는 오차함수)
기대값
$$E(X) = 0$$
중앙값
$$ Mdn = 0 $$
최빈값
$$ Mo = 0 $$
분산
$$Var(X) = 1$$
왜도
$$ \gamma_{1} = 0 $$
첨도
$$ \gamma_{2} = 0 $$
타 분포와의 관계
참고사항
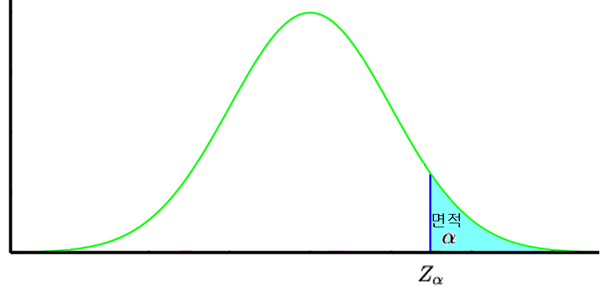
표준정규분포에서 $Z_{\alpha}$는 아래와 같이 정의 된다.
- $$ \alpha = 1 - F(Z_{\alpha}) $$
- $$ \alpha = \int^{\infty}_{Z_{\alpha}} \frac{1}{\sqrt{2\pi}} e^{-\frac{x^{2}}{2}} \ dx $$
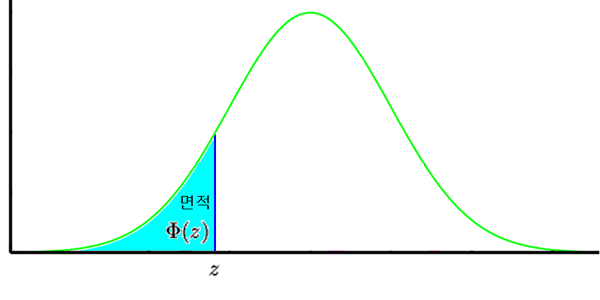
표준정규분포에서 $\Phi (a)$는 아래와 같이 정의 된다.
- $$ \Phi (z) = F(z) $$
- $$ \Phi (z) = \int^{z}_{-\infty} \frac{1}{\sqrt{2\pi}} e^{-\frac{x^{2}}{2}} \ dx $$