meta data for this page
계수 규준형 2회 샘플링 검사
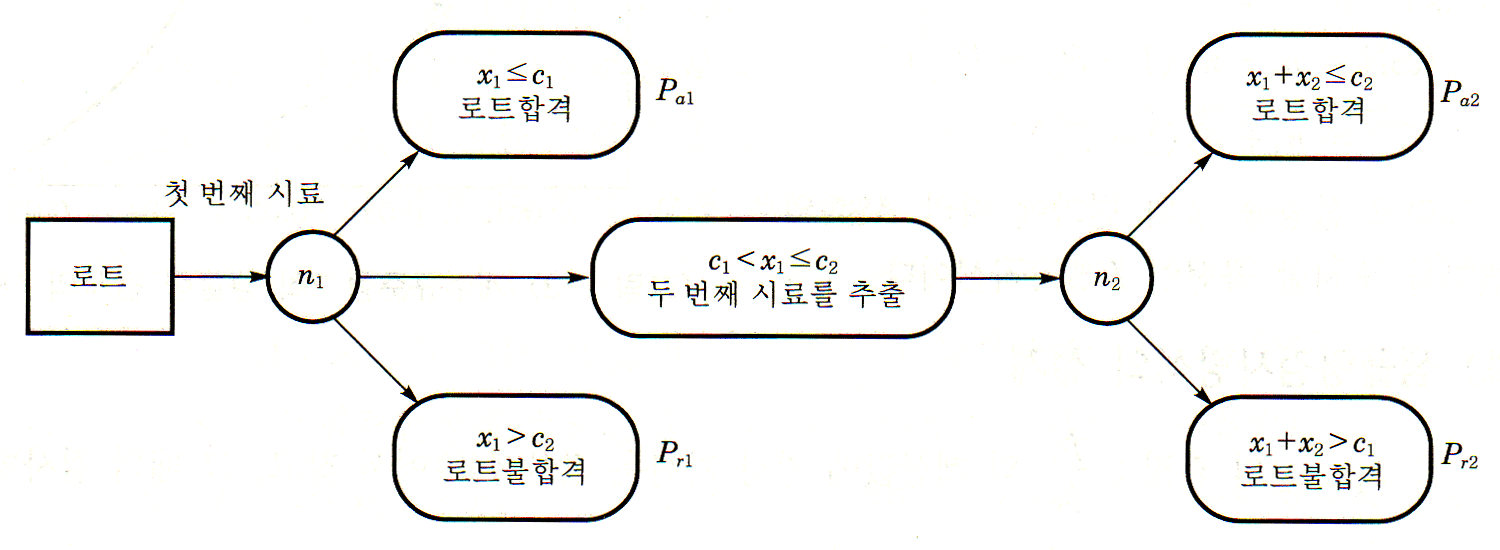
계수 규준형 2회 샘플링 검사는 로트에서 첫 번째 샘플을 뽑아, 그 중의 불량품의 개수를 가지고, 로트 그 자체의 합격, 불합격 또는 두번째 샘플을 뽑을지 판단을 하고 두번째 샘플을 뽑아야 할 필요가 있을 경우 미리 정의된 수만큼 샘플을 뽑아 다시 로트의 합격, 불합격을 판정하는 샘플링 검사로서, 파는 사람에 대한 보호와 사는 사람에 대한 보호를 규정하여, 파는 사람과 사는 사람 양편의 요구를 만족하도록 짜놓은 검사이다.
| $N$ | 로트의 크기 |
| $n_{i}$ | $i$ 차 샘플의 크기 $(i=\{1,2\})$ |
| $c_{i}$ | $i$ 차 샘플에서 합격판정 개수 $(i=\{1,2\})$ |
| $x_{i}$ | $i$ 차 샘플에서 추출한 불량품의 수 $(i=\{1,2\})$ |
| $p$ | 로트의 불량률 |
| $p_{0}$ | 되도록 합격시키고 싶은 로트의 불량률의 상한(AQL) |
| $p_{1}$ | 되도록 불합격시키고 싶은 로트의 불량률의 하한(RQL) |
| $\alpha$ | 불량률 $p_{0}$ 와 같은 품질이 좋은 로트가 샘플링 검사에서 불합격이 되는 확률 (제1종과오) |
| $\beta$ | 불량률 $p_{1}$ 과 같은 품질이 나쁜 로트가 샘플링 검사에서 합격이 되는 확률 (제2종과오) |
| $L_{i}(p)$ | 불량률이 $p$ 인 로트가 $i$ 차 샘플에서 합격할 확률 $(i=\{1,2\})$ |
| $L(p)$ | 불량률이 $p$ 인 로트가 합격할 확률 |
| $R_{i}(p)$ | 불량률이 $p$ 인 로트가 $i$ 차 샘플에서 불합격할 확률 $(i=\{1,2\})$ |
| $R(p)$ | 불량률이 $p$ 인 로트가 불합격할 확률 |
로트의 합격 확률
계수 규준형 2회 샘플링 검사에서 1차 샘플에서 로트가 합격될 확률
- $$L_{1}(p)=P\{ X_{1} \leq c_{1} \}= \sum_{x=0}^{c_{1}} P \{ X_{1}=x \}$$
계수 규준형 2회 샘플링 검사에서 2차 샘플에서 로트가 합격될 확률
- $$L_{2}(p)=P\{ c_{1} < X_{1} \leq c_{2} \ , \ X_{1}+X_{2} \leq c_{2} \}= \sum_{x=c_{1}+1}^{c_{2}} P \{ X_{1}=x \} P \{ X_{2} \leq c_{2}-x \}$$
계수 규준형 2회 샘플링 검사에서 로트가 합격될 확률
- $$L(p)=L_{1}(p)+L_{2}(p)$$
로트의 불합격 확률
계수 규준형 2회 샘플링 검사에서 1차 샘플에서 로트가 합격될 확률
- $$R_{1}(p)=P\{X_{1}>c_{2}\}=1-\sum_{x=0}^{c_{2}}P{X_{1}=x}$$
계수 규준형 2회 샘플링 검사에서 2차 샘플에서 로트가 합격될 확률
- $$R_{2}(p)=1-L_{1}(p)-L_{2}(p)-R_{1}(p)$$
계수 규준형 2회 샘플링 검사에서 로트가 합격될 확률
- $$R(p)=1-L(p)$$
평균 샘플개수
단축 검사를 실시하지 않을 경우
- $$ ASN = n_{1} P_{1} + (n_{1} + n_{2})(1-P_{1}) = n_{1} + n_{2} (1 - P_{1}) $$
단, 여기서 $P_{1}$은 1회 샘플링 검사에서 로트의 합격 불합격 여부가 판정될 확률로 $P_{1} = L_{1}(p) + R_{1}(p)$와 같음
단축 검사를 실시 할 경우
- $$ASN = $$