meta data for this page
문서의 이전 판입니다!
계수 규준형 축차 샘플링 검사
정의
[계수 규준형 축차 샘플링 검사]란 [로트]로부터 1개씩 시료를 채취하여 시험해 가면서 누계 불량개수를 합격 또는 불합격 판정개수와 비교함으로써 [로트]의 합격 또는 불합격을 결정하는 [샘플링 검사]로서, 생산자와 소비자가 요구하는 검사특성을 만족시키면서 [평균샘플개수]가 최소로 되도록 설계한 것이다.
| $D$ | 누계불량개수 |
| $A$ | 합격판정개수 |
| $R$ | 불합격판정개수 |
| $d_{_{0}}$ | 합격판정선 |
| $d_{_{1}}$ | 불합격판정선 |
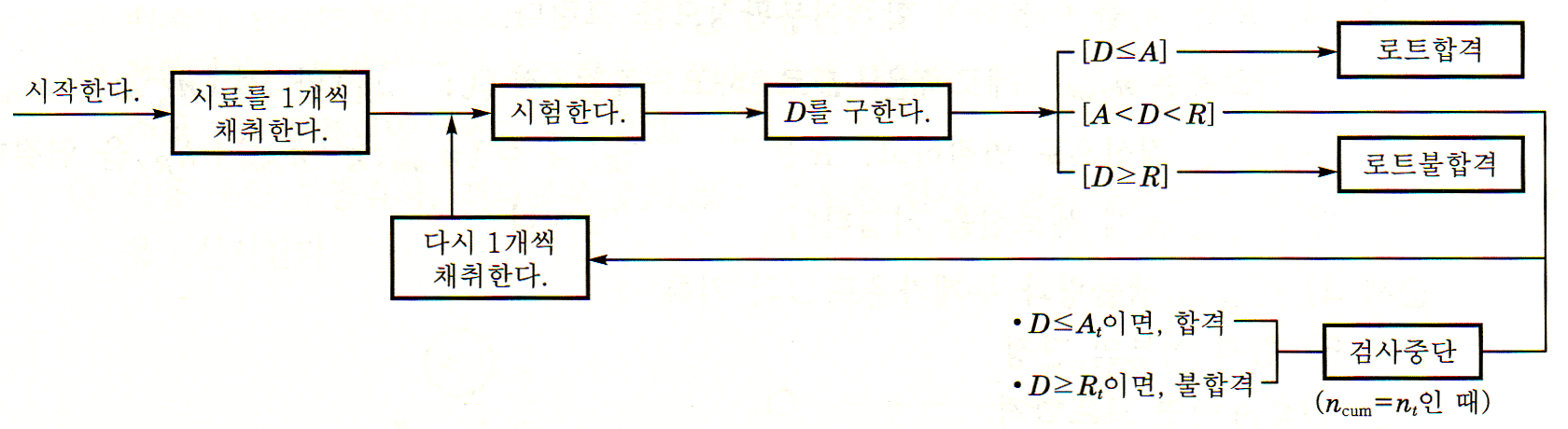
검사의 절차
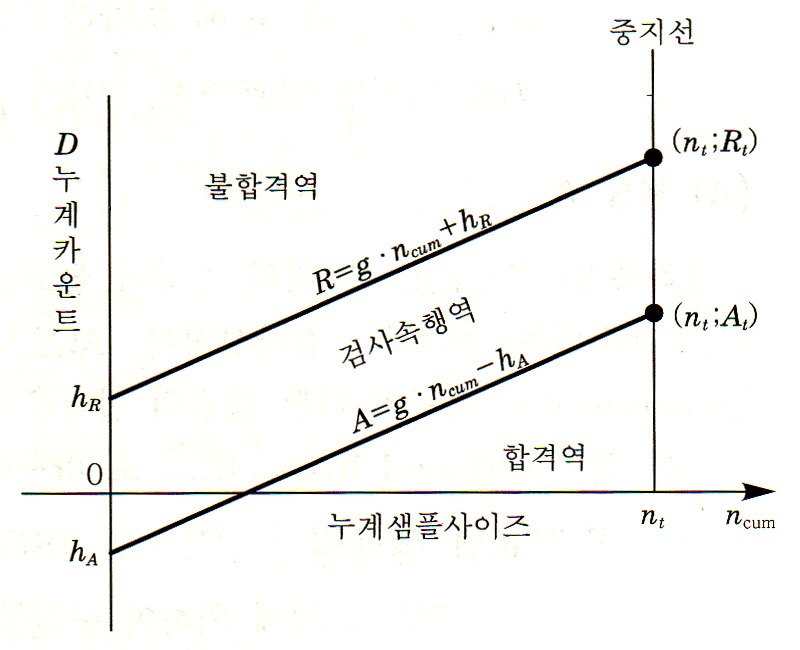
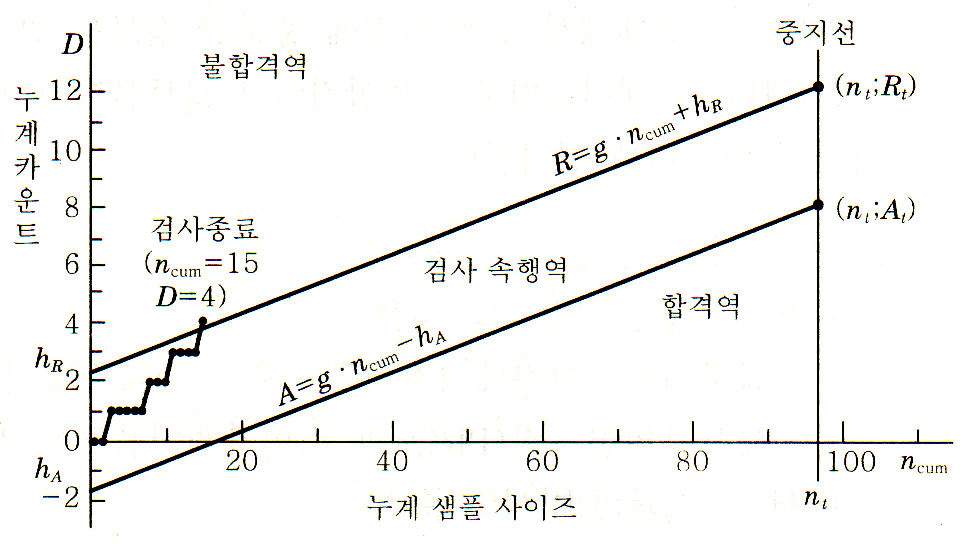
$$ A = g \cdot n_{cum} - h_{A} $$
$$ R = g \cdot n_{cum} + h_{R} $$
$$ h_{A} = \log \frac{1-\alpha}{\beta} / \log \left\{ \frac{p_{_{1}}(1-p_{_{0}})}{p_{_{0}}(1-p_{_{1}})} \right\} $$
$$ h_{R} = \log \frac{1-\beta}{\alpha} / \log \left\{ \frac{p_{_{1}}(1-p_{_{0}})}{p_{_{0}}(1-p_{_{1}})} \right\} $$
$$ g = \log \frac{1-p_{_{0}}}{1-p_{_{1}}} / \log \left\{ \frac{p_{_{1}}(1-p_{_{0}})}{p_{_{0}}(1-p_{_{1}})} \right\} $$
$D \leq A$이면 로트 합격
$D \geq R$이면 로트 불합격
$A < D < R$이면 검사속행
로트의 합격 확률
| $p$ | $L(p)$ |
|---|---|
| $0.00$ | $1.00$ |
| $p_{_{0}}$ | $1-\alpha$ |
| $g$ | $$h_{R}/(h_{A}+h_{R})$$ |
| $p_{_{1}}$ | $\beta$ |
| $1.00$ | $0.00$ |
평균 샘플개수
| $p$ | $ASN$ |
|---|---|
| $0.00$ | $\frac{h_{A}}{g}$ |
| $p_{_{0}}$ | $$ \frac{(1-\alpha)h_{A} - \alpha h_{R}}{g-p_{_{0}}} $$ |
| $g$ | $$\frac{h_{A}h_{R}}{g(1-g)}$$ |
| $p_{_{1}}$ | $$ \frac{(1-\beta)h_{R} - \beta h_{A}}{p_{_{1}}-g} $$ |
| $1.00$ | $$\frac{h_{R}}{1-g}$$ |