meta data for this page
감마분포 (Gamma Distribution)
정의
- 지수분포의 확장판
표기
$\alpha$ : 모양 매개변수
$\beta$ : 크기 매개변수
$$ X \sim G(\alpha , \beta)$$
- $$ \alpha \in ( \ 0 \ , \ \infty \ ) $$
- $$ \beta \in ( \ 0 \ , \ \infty \ ) $$
받침
$$ x \in [ \ 0 \ , \ \infty \ ) $$
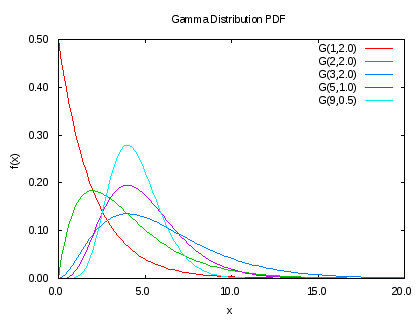
확률밀도함수
$$ f(x) = \left[ \frac{1}{\Gamma(\alpha) \cdot \beta^\alpha} \right] \cdot x^{\alpha-1} \cdot e^{-x/\beta} $$
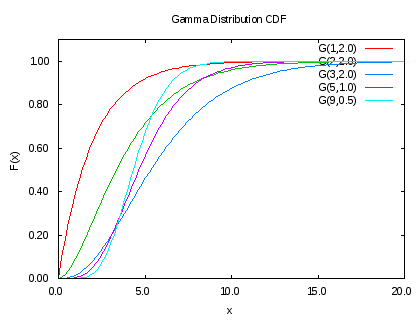
누적분포함수
$$ F(x) = P \left( \ \alpha \ , \ \frac{x}{\beta} \ \right) $$
단, $P \left( \ a \ , \ b \ \right)$는 정칙 감마함수이다.
기대값
$$ E(X) = \alpha \beta $$
최빈값
$$ Mo = (\alpha - 1) \beta $$
분산
$$ Var(X) = \alpha \beta^{2} $$
왜도
$$ \gamma_{1} = \frac{2}{\sqrt{\alpha}} $$
첨도
$$ \gamma_{2} = \frac{6}{\alpha} $$
특성함수
$$ \phi \ (t) = (1-\beta \cdot i \cdot t)^{-\alpha} $$
적률생성함수
$$ M(t) = (1-\beta \cdot t)^{-\alpha} $$
특징
- 재생성을 가진다.
- $X_{i} \sim G(\alpha_{i},\beta)$이면 $\sum X_{i} \sim G(\sum \alpha_{i},\beta)$이 성립한다.