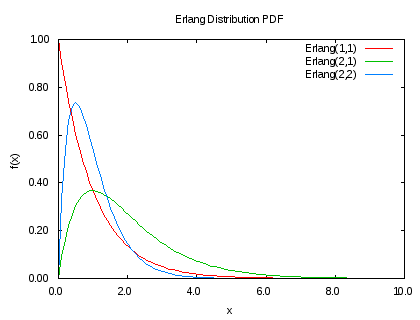
어랑분포 (Erlang Distribution)

어랑분포는 포아송과정에서 $n$번째 사건이 발생할 때까지 걸리는 시간의 분포이다. 사건 발생간격시간은 지수분포이므로 어랑분포는 지수분포 확률변수들의 합의 분포가 된다.

지수분포, 정규분포, 균일분포, 와이블분포 등과 비슷한 분포인 어랑분포는 연속 확률 변수에서 파생된 분포이다. 이 분포는 덴마크의 수학자인 Agner Krarup Erlang 에서 이름을 따왔다. 이 덴마크의 수학자는 코펜하겐 전화국에서 전화의 지연과 손실에 대한 문제에 대해서 일하고 있었다. A.K. Erlang 은 1909 년에 자신의 첫번째 논문인 The theory of probability and telelphone conversations 에서 이 문제에 대해 자세히 설명했다.

$$X \sim Erlang( \ n \ , \ \lambda \ )$$

$$x \in [ \ 0 \ , \ \infty \ )$$

$$f(x) = \frac{\lambda^{n} \cdot x^{n-1}}{\Gamma(n)} \cdot e^{- \lambda \cdot x}$$

$$\begin{displaymath}\begin{split} F(x) &= 1 - \sum_{k=0}^{n-1} e^{-\lambda \cdot x} \frac{(\lambda \cdot x)^{k}}{k!} \\ &= 1 - \frac{\Gamma(n,x \cdot \lambda)}{\Gamma(n)} \end{split}\end{displaymath}$$ <plot> set title "Erlang Distribution CDF" set size 1.0 set xrange [0:10] set yrange [0:1.1] set format x "%.1f" set format y "%.2f" set xlabel "x" set ylabel "f(x)" cerlang(x,n,lambda)=(igamma(n,x*lambda))/(gamma(n)) plot cerlang(x,1,1.0) title "Erlang(1,1)", \ cerlang(x,2,1.0) title "Erlang(2,1)", \ cerlang(x,2,2.0) title "Erlang(2,2)" </plot> ===== 기대값 ===== $$E(X) = \frac{n}{\lambda}$$ ===== 최빈값 ===== $$Mo = \frac{n-1}{\lambda}$$ ===== 분산 ===== $$Var(X) = \frac{n}{\lambda^{2}}$$ ===== 왜도 ===== $$\gamma_{1} = \frac{2}{\sqrt{k}}$$ ===== 첨도 ===== $$\gamma_{2} = \frac{6}{n}$$ ===== 특성함수 ===== $$\phi (t) = \left( 1-\frac{i \cdot t}{\lambda} \right)^{-n}$$ ===== 적률생성함수 ===== $$M(t) = \left( 1-\frac{t}{\lambda} \right)^{-n}$$

단, $n< \lambda$인 경우에만 성립

• 분포